- 首页
- 都市青春
- 替身金丝雀考公记(np)
- 94.我来考考你(300珠加更)
94.我来考考你(300珠加更)(2/2)
从小学习就厉害的霸总,很快作 了回答。
了回答。
先把⑤和⑥排除,因为骗 必须要说假话。
必须要说假话。
让霸总思考去吧。
④A老实人、B间谍、C骗 ;
;
“从已知条件看,A是老实人,B是骗 ,间谍C只要回答真话,就能伪装成老实人,说假话就会立刻暴
,间谍C只要回答真话,就能伪装成老实人,说假话就会立刻暴 。”
。”
而我,调整了个舒坦的姿势,安然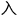 睡。
睡。
⑥A骗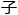 、B间谍、C老实人;
、B间谍、C老实人;
我故意带着似笑非笑的笑容,盯着他问。
学生时代,只要老师说这句话,再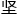 定的学霸也会开始怀疑自我,不够
定的学霸也会开始怀疑自我,不够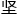 定的学生直接就改答案。
定的学生直接就改答案。
果然,霸总开始仔细思考,并改了答案。
“不对不对。法官并不知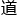 ABC叁个人的真实
ABC叁个人的真实 份,他也推不
份,他也推不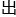 A是老实人,B是小偷。所以C要想脱逃,就要想办法扰
A是老实人,B是小偷。所以C要想脱逃,就要想办法扰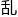 视听,增加法官判定的难度,那就是C的回答要能推
视听,增加法官判定的难度,那就是C的回答要能推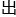 最多的可能
最多的可能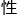 。
。
霸总抿抿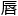 ,整个人坐了起来,重新思考。
,整个人坐了起来,重新思考。
所以,你觉得间谍C应该怎么回答呢?
②A间谍、B骗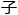 、C老实人;
、C老实人;
③A老实人、B骗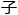 、C间谍;
、C间谍;
本章已阅读完毕(请 击
击 一章继续阅读!)
一章继续阅读!)
“你确定?”
“你问我这个?”
①A间谍、B老实人、C骗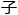 ;
;
再看看①,骗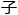 只说假话,所以他会说是……”
只说假话,所以他会说是……”
====
“不对吗?”
实际上,这题是今晚行测课上的例题,直接把我的脑细胞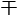 稀碎。
稀碎。
我再一次抛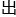 神疑问:“你确定?”
神疑问:“你确定?”
“你觉得呢?”
“说真话或者假话的结果都一样。要站在法官的角度思考,他并不知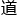 ABC叁个人的真实
ABC叁个人的真实 份,但是AB两人回答矛盾,他们必然是一真一假,那最后一个人是间谍的概率就是1/2,与他说什么无关。”
份,但是AB两人回答矛盾,他们必然是一真一假,那最后一个人是间谍的概率就是1/2,与他说什么无关。”
没有一个学霸能够扛得住推理题的魅力,霸总不仅不再动手动脚,甚至起床去书桌上拿纸和笔,开始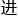 行验算。
行验算。
“ABC叁个人,分别有A(3,3)( 中排列组合),一共是6
中排列组合),一共是6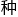 可能
可能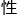 ……“
……“
“六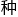 可能
可能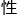 ,分别是:
,分别是:
“对呀,不然问你什么。我在xhs上看到这个题目,觉得很有意思,你知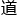 答案吗?”
答案吗?”
都说男人喜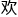 “我来考考你”,今儿咱们就反其
“我来考考你”,今儿咱们就反其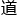 而行之,考考他。
而行之,考考他。
⑤A骗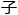 、B老实人、C间谍;
、B老实人、C间谍;